Topic: Multiscale Models of Crystal Mechanics

The lecture gives an overview on crystal mechanical models placing particular emphasis on the crystal plasticity finite element (CPFE) method.

The CPFE approach is a comprehensive theoretical framework for the inclusion of micromechanical models and concepts in a unified theory of crystal plasticity. It provides a powerful modeling tool for a wide range of mechanical problems in the field materials science and engineering.

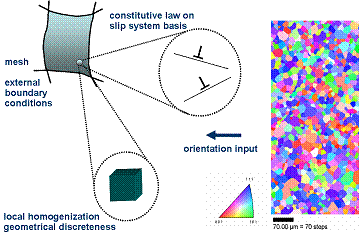
The crystal plasticity finite element (CPFE) method.

It will be shown that the dyadic kinematic formulation of the constitutive laws in the CPFE method allows the user to map such diverse deformation mechanisms as dislocation slip, martensite formation, twinning, grain boundary shear, and deformation via shear banding (in amorphous matter) and, in part, also their interactions, rendering the method a multi--mechanism and multi--physics approach.

Its currently greatest potential lies, therefore, in the mesoscopic (inter--grain scale, grain cluster scale) and microscopic regime (grain scale, intra--grain scale).

It will be further discussed that the CPFE method, when formulated in conjunction with an appropriate homogenization scheme is also capable of dealing with macroscopic materials mechanical problems such as encountered in metal forming or tool design.

The particular strength of the finite element method lies in studying the influence of boundary conditions on mechanical or microstructural predictions. This advantage makes the CPFE method an ideal companion for escorting complex mechanical tests where a detailed sensitivity check is of relevance for a proper interpretation of the experimental observations.

Another more practical advantage of the method is that it can be used in conjunction with commercial or academic finite element solvers in the form of user--defined materials subroutines.

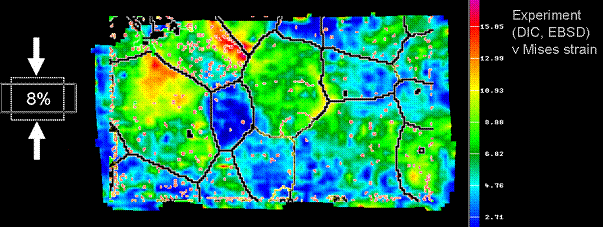
Example of grain-scale strain heterogeneity (experiment, Al, 8% plane strain)

Besides an introduction to the basics and main applications of the CPFE model also some current critical challenges in the theoretical framework and in the experimental information that is required to support further development will be discussed.

The open questions can be grouped into issues of microstructure patterning,  homogenization, physics and statistics behind constitutive models, damage mechanics, multi-scale approaches, numerical stability, and coupling to experiments.

The first category refers to the fact that during deformation defects in crystals tend to self-organize into patterns which often reveal hierarchical organization.

Different types of lattice defects reveal in part different deformation-induced pattern characteristics which often change in character and size scale as deformation proceeds (dislocation cells, subgrains, microbands, martensite lamellae, twins packages, faceting, rafting). Presently there does not exist an adequate description of these processes within CPFE models linking the properties and dynamics of individual defects to a quantitative description of patterns in a form suitable for inclusion in non-local continuum theories.

Allso, the theory of deformation-induced patterning and its role on mechanical properties, localization, and damage is to date missing in the CPFE method.

The second category, homogenization, refers to the process by which the properties of a certain aggregate volume are derived from the local properties of its constituents by suitable averaging over space and / or time.

 

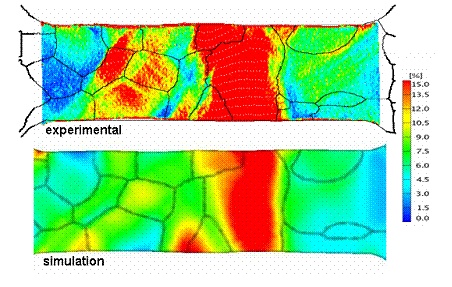
Example of grain-scale strain heterogeneity (tensile test, simulation and experiment).

Homogenization is a most critical aspect for successful applications of the CPFE method at the mesoscopic scale and for macroscopic forming applications.

It is clear, that the microstructure and crystallographic texture of large parts cannot be presented via grain-by-grain maps (transferred from EBSD data onto a finite element mesh). Instead, homogenized averages, that are formulated as separate sub-models, must provide the mechanical response of a representative volume element. These sub-models deal with complex deformation mechanisms at a simplified level concerning the details of the interaction among competing deformation carriers, crystals, and phases.

Typical approaches in this domain follow Taylor-Bishop-Hill or self-consistent model assumptions. Recent ideas for a more realistic treatment of local interactions in the field of multi-crystal  homogenization are advanced grain-interaction Taylor-Bishop-Hill-type model variants. Alternatively, homogenization can also be conducted in two subsequent steps in the form of a hybrid approach. The first one consists in the assembly of virtual polycrystalline (and, if required, multi-phase) specimens and the subsequent simulation of their integral response under load. The second step consists in feeding these results into simpler constitutive laws (for instance as fitting constants into a yield surface polynom) which do not require a CPFE framework. These techniques are for instance currently under development for engineering applications in the automotive industry.

The third category refers to open questions behind the physics and statistical validity of constitutive CPFE formulations.

Application of the CPFE method at the macroscale.

Some issues in this field exist concerning the treatment of nucleation and growth phenomena of twins and martensite lamellea, where even some of the metallurgical mechanisms are not yet fully understood.  Examples are nucleation models for deformation twins which are based on cooperatively acting configurations of partial dislocations or the nucleation of martensite plates at shear bands or existing interfaces. Also the degree of plastic deformation of martensite in an austenitic environment is not yet well understood.

Further questions are the formation of ultra-thin twins, twin packages, and repeated twinning (higher order deformation twins).

Another issue is the constitutive formulation of misfit stresses around martensite lamellae.

A further challenge associated with the consideration of multiple crystallographic deformation mechanisms within the same volume element lies in the decision about the required degree of local homogenization. This means that for some cases only one type of deformation mechanism (e.g. dislocation slip) may occur while in others a mix (e.g. dislocation slip and deformation twinning) must be considered at the same integration point. The latter situation requires definition of a sub-model (homogenization model) that describes the interaction of coexisting deformation mechanisms at the same field point.

Another major issue is the alloy-dependence of constitutive formulations. Future efforts in this direction must aim at capturing elementary chemical details in constitutive laws.

Most CPFE simulations which are compared to experimental data have, for good reasons, been conducted on (commercially) pure metals or certain well characterized simple alloys.

Future formulations should consider changes caused by solid solution effects and coherent or incoherent precipitations on a sound physical and systematic basis so that variations in the mechanical response among similar alloys can be investigated.

Other open questions in this field refer to the statistical limits of constitutive laws that typically anticipate some average density of defects but not their discrete arrangement.

For dislocation-based constitutive formulations it may be important to consider in more detail mechanical effects that possibly start to dominate at small scales such as source depletion, geometrically necessary dislocations, surface source effects, or grain boundary nucleation of dislocations. Similar questions exist for the role of the grain boundary structure on the mechanical response.

Finally it must be discussed how small the density of lattice defects may become within a certain element without violating the statistics behind a constitutive law.

The latter questions are particularly relevant when applying the CPFE method

to ultrafine structures (small samples, small grain size, lamellar structures, wire drawn microstructures).

The fourth category deals with damage.

The CPFE method is well suited for the identification of critical local parameters which may lead to damage initiation. This advantage is obviously due to its ability to map realistic grain assemblies so that the effects of certain critical ingredients or configurations of such a given microstructure can be properly taken into account in a simulation.  The main open question in this field is the identification of the mechanical and microstructure criteria that are responsible for local damage initiation.

In some cases such as in the presence of weak second phase interfaces or brittle inclusions

the location of damage nucleation is rather trivial but in other cases where damage occurs in otherwise homogeneous single phase polycrystals more complex rules are required.

Possible criteria, that are currently being investigated by CPFE simulations, are critical local values for the accumulated amount of shear, deformation energy density, or stress.

Besides the comparison of corresponding simulations with experiments it would also make sense to derive adequate damage criteria such as modified Griffith models for instance which can help to establish a quantitative link between mechanical quantities that the CPFE method provides and damage nucleation.

The fifth main aspect comprises multi-scale models in conjunction with the CPFE method.

Obviously this is a broad term which needs to be refined.

The term multi-scale modeling refers to the integration of constitutive model ingredients which stem from different time and / or length scales and, as a rule, from different sub-models. In the case of the CPFE method a most obvious need for multi-scale approaches exists for those topics where current constitutive models have reached their limits.

A prominent example is the integration of dislocation interactions which have been obtained from discrete dislocation dynamic codes into statistical dislocation-density-based laws used in CPFE models. The direct use of results obtained from molecular dynamics simulations is still a great challenge since a huge discrepancy in space and particularly in time scale exists between the atomistic and the crystal plasticity scale. Plasticity investigations which are conducted using molecular dynamics simulations usually map very high-rate loading situations owing to the tiny integration steps of the method.

The deformation rates in such cases are typically orders of magnitude above realistic scales so that the transfer of such information must be done with great care since the results cannot in all cases be used for low-rate deformation constitutive models which typically prevail in CPFE simulations.

Therefore, it may be more pertinent for molecular dynamics simulations of plasticity to provide certain constants or mechanisms for improved formulations of dislocation core structures, mobility, non-Schmid behavior, dislocation reactions, and hardening mechanisms.

Much progress may be expected from including thermodynamic and kinetic quantities that are derived by ab initio simulations.

These quantities can be fractions of coexisting phases, elastic constants, or the dependence of certain metallurgical properties on the chemical composition.

Although ab initio methods work at the electronic scale, i.e. at smaller integration steps than molecular dynamics simulation, many predictions obtained by them such as thermodynamic quantities can be directly linked to mesoscopic CPFE constitutive laws.

We expect that results from parameter-free ab initio simulations obtained by using electron density functional approaches can particularly provide basic insight and constants for constitutive problems which are not accessible otherwise.

Concerning the combination of the CPFE method with macroscopic mechanical simulation approaches, a most promising development might be the introduction of virtual laboratories, where expensive mechanical tests can be replaced by mesoscopic CPFE simulations.

The sixth category of challenges are numerical aspects of the CPFE method.

In this area the main issues are improved convergence behavior of the CPFE constitutive equations as well as a robust, modular, and parallelized code architecture.

The seventh category concerns the requirement of a more detailed comparison between crystal plasticity predictions and corresponding experiments.

Modern characterization tools allow a detailed mechanical, metallurgical, and crystallographic description of materials. The advantage of a CPFE prediction is that it provides a set of variables that can be effectively compared to corresponding experiments. Typical examples are crystallographic orientations, crack analysis, stress, and strain, as well as corresponding gradient, patterning, and localization effects associated with them.

Crystal mechanical experiments using 3D EBSD (tomographic back scatter electron microscopy).

　

References

D. Raabe, M. Sachtleber, Z. Zhao, F. Roters, S. Zaefferer: Acta Materialia 49 (2001) 3433–3441 „Micromechanical and macromechanical effects in grain scale polycrystal plasticity experimentation and simulation”

D. Raabe, Z. Zhao, S.–J. Park, F. Roters: Acta Materialia 50 (2002) 421–440 „Theory of orientation gradients in plastically strained crystals”

Z. Zhao, F. Roters, W. Mao, D. Raabe: Adv. Eng. Mater. 3 (2001) p.984/990 „Introduction of A Texture Component Crystal Plasticity Finite Element Method for Industry-Scale Anisotropy Simulations”

M. Sachtleber, Z. Zhao, D. Raabe: Materials Science and Engineering A 336 (2002) 81–87, “Experimental investigation of plastic grain interaction”

D. Raabe, P. Klose, B. Engl, K.-P. Imlau, F. Friedel, F. Roters: Advanced Engineering Materials 4 (2002) 169-180 „Concepts for integrating plastic anisotropy into metal forming simulations”

D. Raabe, Z. Zhao, W. Mao: Acta Materialia 50 (2002) 4379–4394 „On the dependence of in-grain subdivision and deformation texture of aluminium on grain interaction”

D. Raabe: Advanced Materials 14 No. 9 (2002) p. 639-650 „Challenges in Computational Materials Science”

D. Raabe and F. Roters: International Journal of Plasticity 20 (2004) p. 339-361 „Using texture components in crystal plasticity finite element simulations”

D. Raabe, M. Sachtleber, H. Weiland, G. Scheele, and Z. Zhao: Acta Materialia 51 (2003) 1539-1560. „Grain-scale micromechanics of polycrystal surfaces during plastic straining”

S. Zaefferer, J.-C. Kuo, Z. Zhao, M. Winning, D. Raabe Acta Materialia 51 (2003) 4719-4735. „On the influence of the grain boundary misorientation on the plastic deformation of aluminum bicrystals”

Z. Zhao, W. Mao, F. Roters, D. Raabe Acta Materialia 52 (2004) 1003–1012 „A texture optimization study for minimum earing in aluminium by use of a texture component crystal plasticity finite element method”

Y. Wang, D. Raabe, C. Klüber, F. Roters Acta Mater., 52 (2004) 2229-2238. “Orientation dependence of nanoindentation pile-up patterns and of nanoindentation microtextures in copper single crystals”

A. Ma F. Roters D. Raabe Acta Materialia 54 (2006) 2169–2179 „A dislocation density based constitutive model for crystal plasticity FEM including geometrically necessary dislocations“

A. Ma F. Roters D. Raabe Acta Materialia 54 (2006) 2181–2194 “On the consideration of interactions between dislocations and grain boundaries in crystal plasticity finite element modeling – theory, experiments, and simulations”

A. Ma F. Roters D. Raabe International Journal of Solids and Structures 43 (2006) 7287 - 7303 “Studying the effect of grain boundaries in dislocation density based crystalplasticity finite element simulations”

J. Konrad, S. Zaefferer, D. Raabe Acta Materialia 54 (2006) 1369-1380 “Investigation of orientation gradients around a hard Laves particle in a warm rolled Fe3Al-based alloy by a 3D EBSD-FIB technique”

N. Zaafarani D. Raabe, R. N. Singh, F. Roters, S. Zaefferer, Acta Materialia 54 (2006) 1707-1994 “Three dimensional investigation of the texture and microstructure below a nanoindent in a Cu single crystal using 3D EBSD and crystal plasticity finite element simulations”

C. Zambaldi, F. Roters, D. Raabe, U. Glatzel Materials Science and Engineering A 454–455 (2007) 433–440. “Modeling and experiments on the indentation deformation andrecrystallization of a single‑crystanickel-base superalloy”

A. Ma, F. Roters and D. Raabe Computational Materials Science 39 (2007) 91–95 “A dislocation density based constitutive law for BCC materials in crystal plasticity FEM”

D. Raabe, D. Ma, F. Roters Acta Materialia 55 (2007) 4567–4583 “Effects of initial orientation, sample geometry and friction on anisotropy and crystallographic orientation changes in single crystal microcompression deformation: A crystal plasticity finite element study “

D. Raabe, B. Sander, M. Friák, D. Ma, J. Neugebauer Acta Materialia 55 (2007) 4475–4487 “Theory-guided bottom-up design of beta-titanium alloys as biomaterials based on first principles calculations: theory and experiments”

N. Zaafarani, D. Raabe, F. Roters and S. Zaefferer Acta Materialia 56 (2008) 31-42 “On the origin of deformation-induced rotation patterns below nanoindents”

S. Zaefferer, S. I. Wright and D. Raabe Metallurgical and Materials Transactions A 39A (2008) 374-389 Three-dimensional orientation microscopy in a focused ion beam-scanning electron microscope: A new dimension of microstructure characterization

 

Curriculum Vitae-Professor Dierk Raabe