我国科学家在NP完全问题计算复杂性的研究方面取得重要进展。中国科学院金属研究所张志东研究员确定了背包问题的计算复杂度下限。论文发表在AIMS Mathematics 10 (2025) 11918-11938。

随着计算机领域的技术进步，人工智能正在影响我们日常生活的方方面面。而人工智能的进步依赖于计算算法的速度。如何在最短时间内算出正确的解是计算机领域科学家最关心的问题。NP完全问题是计算机科学中非常重要的难题。在计算复杂性理论中，NP表示非确定性多项式时间，NP问题定义为在一个非确定性图灵机上以多项式时间求解的决定性问题的集合。P问题是在确定性图灵机上以多项式时间求解的问题的集合。在NP中，以多项式时间确认解的决定性问题的集合归类为NP完全问题。在NP中所有其他问题都可以在多项式时间内约化为NP完全问题（以及其特例）。著名的NP完全问题有：布尔可满足性问题、旅行推销员问题、背包问题、哈密顿环问题、子集和问题、顶角覆盖问题、子图同构问题、独立集合问题、图着色问题、蛋白质折叠问题、自旋玻璃问题等。这一类非平凡难题的共同特征是具有随机性的模型系统中存在非平庸拓扑结构、非平面性图、非局域性或长程自旋纠缠。

针对N个具有固定权重和价值的二元变量的决定性问题，背包问题的目标是，在限制所有物体权重之和小于或者等于最大权重的前提下，最大化所有物体的价值之和。背包问题可以用来进行组合数学、密码学、商业等领域的计算，还可以应用在不同领域的决策，如寻找减少原材料使用、投资组合的选择、密钥产生等最优化搜寻路径。背包问题与自旋玻璃模型的联系：背包问题的二元决定性变量对应于自旋向上和自旋向下两种状态。背包问题的权重对应于自旋之间的相互作用。背包问题的哈密顿量可以映射成具有偏置场的自旋玻璃模型的哈密顿。所以，可以通过求解自旋玻璃模型求解背包问题。在背包问题中最大化所有物体的价值之和等价于在自旋玻璃模型中最小化自由能。

张志东首先分析了NP完全问题中非平庸拓扑结构的起源。从自旋玻璃三维伊辛模型出发，详细地阐明三维晶格上自旋排列与统计物理中转移矩阵的二维特征之间的矛盾导致非平庸拓扑结构。确认自旋玻璃三维伊辛模型存在绝对极小核心(AMC)模型，为一层晶格自旋玻璃伊辛模型与其最近邻层自旋的相互作用。它等于两层晶格自旋玻璃三维伊辛模型减去一个自旋玻璃二维伊辛模型。用蛮力搜索绝对极小核心模型决定了其计算复杂度的下限。并且，确认自旋玻璃三维伊辛模型中存在NP中间问题，给出体系的计算复杂度的相图。绝对极小核心模型存在于NP完全问题和NP中间问题的边界上。进一步地，根据自旋玻璃三维伊辛模型和背包问题之间的映射，证明背包问题同样存在绝对极小核心模型和NP中间问题，也给出背包问题的计算复杂度相图。并且证明了背包问题的计算复杂度的下限是亚指数、超多项式的。

本项工作通过物理思想做指导，分析体系的数学结构，提出一个判据，确定了NP完全问题的计算复杂度的下限为(1+无限小)的N次方。本项工作为NP完全问题的数值计算提供了指导性思维，例如通过发展绝对极小核心模型的平行计算，将会极大地优化算法，从目前的1.3的N次方提升至(1+无限小)的N次方。在保持一定计算精度的条件下，用亚指数算法获得复杂系统（如自旋玻璃三维伊辛模型、背包问题等）的精确结果。

本项工作建立了背包问题与自旋玻璃三维伊辛模型的联系，根据两个问题的关系确定了背包问题的计算复杂度的下限。背包问题可以被映射为许多其它的科学问题，所以本项工作的结论可以直接推广应用，解决计算机、物理、化学、生物、数学以及材料科学领域一系列相关基础科学问题。

论文链接

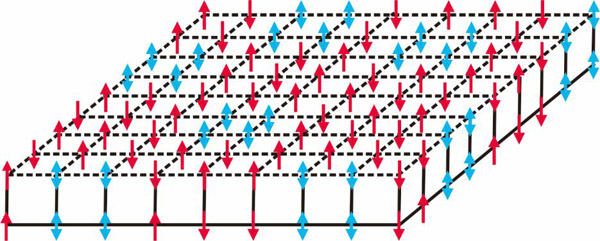
图1.自旋玻璃三维伊辛模型最小核模型示意图，其中红色自旋指向随机分布，并且蓝色自旋存在阻错。

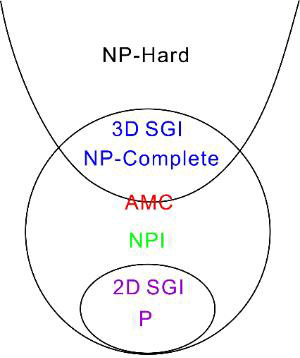
图2. 自旋玻璃三维伊辛模型体系计算度的相图。其中NP中间问题(NPI)在NP完全问题与P问题之间，绝对最小核(AMC)模型在NP完全问题与NP中间问题的边界上。

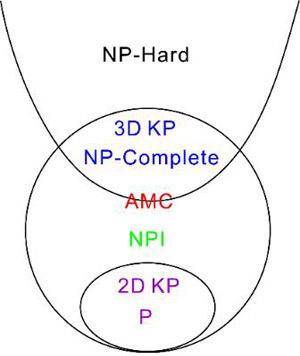
图3. 背包问题计算度的相图。其中NP中间问题(NPI)在NP完全问题与P问题之间，绝对最小核(AMC)模型在NP完全问题与NP中间问题的边界上。

AI读进展：中国科学家破解“背包难题”复杂度之谜：计算速度极限被发现

一、为什么“背包问题”让科学家头疼？

想象你是个准备春游的小学生，书包只能装5斤重的东西。面前有10种零食：薯片（200g，开心值+5）、巧克力（150g，开心值+8）……如何搭配才能既不超过重量，又让你玩得最开心？这就是“背包问题”的童年版。

成年人世界的升级版：

• 如果有100种零食，组合方式会超过宇宙中的原子总数（10^80）
• 传统算法需要检查所有可能组合，耗时指数级增长（比如2^N次操作，N是物品数量）
• 这就是NP完全问题的恐怖之处：问题规模稍大，计算机就算到天荒地老

二、什么是“计算复杂度下限”？

可以理解为解决问题所需的最少时间。比如：

• 整理书包：最低需要1分钟（下限），实际可能需要更久
  
• 背包问题：科学家发现，任何算法至少需要(1+ε)^N 的时间（ε≈0）
  
• 过去认为下限是2^N（指数爆炸）
• 新发现证明存在更优算法（亚指数级），但永远快不过(1+ε)^N
  

类比：

假设你要试遍所有密码锁组合：

• 传统观点：必须试完10000种组合（10^4）
• 新发现：存在一种方法，只需试100.0001种（接近线性增长）

三、物理学家如何用“自旋玻璃”破解数学难题？

自旋玻璃是一种特殊磁性材料，微观磁针（自旋）像一群闹别扭的小朋友：

• 有的磁针想朝上，有的想朝下
• 彼此之间还会互相拉扯（相互作用）
• 整体处于混乱但稳定的状态

科学家的大脑洞：

1. 物品选择 → 磁针方向
背包里“选或不选”一个物品，对应磁针“朝上或朝下”

2. 总价值最大化 → 能量最小化
找到价值最高的组合，等价于让自旋玻璃系统能量最低

3. 三维晶格拓扑 → 计算复杂度来源
发现自旋排列的复杂纠缠结构（类似毛线团打结），是导致计算困难的核心

四、这项研究到底多厉害？

理论层面

• 打破传统认知：证明NP完全问题存在亚指数级算法（介于多项式与指数之间）
• 绘制计算相图：首次明确NP完全问题与稍简单的NP中间问题（如质因数分解）的边界

应用层面

• 密码学：当前加密货币依赖“背包问题很难解”，新算法可能威胁/加固加密体系
• 物流优化：港口集装箱装载效率提升10%~30%
• AI训练：加速神经网络参数搜索，降低算力消耗

五、普通人能感受到什么变化？

• 快递更快：货车装载优化后，你的网购包裹可能早1天到货
• 投资更赚：基金公司用新算法优化投资组合，年化收益提升2%~5%
• 天气预报更准：复杂气候模型计算提速，暴雨预警提前3小时

六、未解之谜：P vs NP 问题

这是计算机领域的终极问题之一，悬赏100万美元（克雷数学研究所）：

• P问题：容易验证答案，也容易求解（比如排序数字）
• NP问题>：容易验证答案，但求解困难（比如背包问题）
• 世纪之问：P=NP吗？如果成立，所有NP问题都能快速求解，密码学将崩溃，AI会飞跃

张志东研究员的研究暗示：

P≠NP。即使P≠NP，NP完全问题也可能存在比传统指数算法更优的解法，为破解P/NP之谜提供新路径。

趣味小测试

假设你的背包能装15kg，有以下物品：
　　- 笔记本电脑（2kg，价值8）
　　- 相机（3kg，价值10）
　　- 金条（10kg，价值30）
　　- 充电宝（1kg，价值3）
　　- 水壶（4kg，价值5）

你能找到总价值最大的组合吗？

这项研究告诉我们：最优化选择不仅需要智慧，还需要突破数学与物理的边界。下次整理行李时，也许可以自豪地说：“我正在解决一个NP完全问题！” 🎒✨

声明：“AI读进展”内容由人工智能技术生成，其内容旨在辅助读者初步了解相关领域研究动态，不代表中国科学院金属研究所正式学术观点或完整研究成果，不作为学术论证依据。